Answer:
Side DE = 32 inches
Step-by-step explanation:
We are given that ΔCDE is similar to ΔQRS, this means that the corresponding sides are equal.
We are also given that the similarity ratio is

Now, we set the similarity ratio and equate it to
 as follows:
as follows:
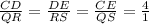
We are given that side RS = 8 inches. Substitute with this value in the above ratio and solve for DE as follows:

DE =
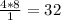 inches
inches
Hope this helps :)