QUESTION 1 ANSWER
The series is
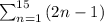
So the nth term of this sequence is
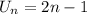
We generate some few terms of the sequence as follows:
When
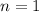 ,
,
The first term of the sequence becomes,
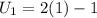
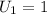
When
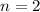 ,
,
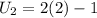
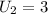
When
 ,
,
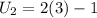
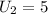
The constant difference is
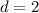 .
.
The sum of the series is given by,
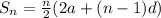
There are 15 terms in the series, therefore

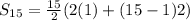
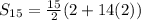
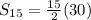
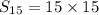
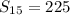
ANSWER TO QUESTION 2
The bottom row has
 boxes. This means
boxes. This means
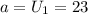
a) Since each row has 3 fewer boxes
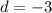 .
.
The nth row is given by,
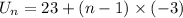
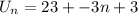
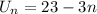
The top row is the 6th row, meaning
 .
.
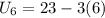
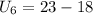
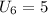
b) The number of boxes in the entire display is given by
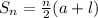
Where
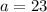 , the first term(row) and
, the first term(row) and
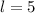 , the last term(row).
, the last term(row).
Since there are 6 rows,
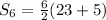
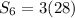
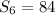
ANSWER TO QUESTION 3
The number of visitors in the first week is
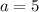 .
.
Since the number of visitors each week is doubled the number of visitors in the subsequent weeks, the sequence is a geometric progression with a common ratio of
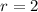 .
.
The general term of a geometric sequence is
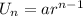
So in the 8th week, we have
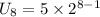

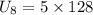
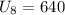
Hence 640 people visited the website in the 8th week