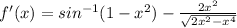Question

(15 Points)

Find the derivative of each of the following (inverse function)

`f(x) = x^2 arctan(x)`

`f(x) = xarcsin(1-x^2)`

Answer 1

ANSWER 1

Note that,

`f(u)=tan^(-1)(u)`

is the same as

`f(u)=arctan(u)`

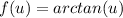
We apply the product rule.

`f(x)=x^2tan^(-1)(x)`

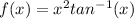
So we keep the second function and differentiate the first,plus we keep the first function and differentiate the second.

`f'(x)=(x^2)'tan^(-1)(x)+x^2(tan^(-1)(x))'`

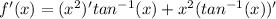
Recall that,

If

`f(u)=tan^(-1)(u)`

Then,

`f'(u)=(1)/(1+u^2)} * u'`

This implies that,

`f'(x)=2xtan^(-1)(x)+(x^2)/(x^2+1)`

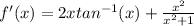
ANSWER 2

We apply the product rule and the chain rules of differentiation here.

`f(x)=xsin^(-1)(1-x^2)`

`f'(x)=x'sin^(-1)(1-x^2)+x(sin^(-1)(1-x^2))'`

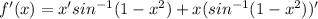
Recall that,

If

`f(u)=sin^(-1)(u)`

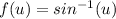
Then,

`f'(u)=(1)/(√(1-u^2)) * u'`

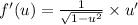
This implies that,

`f'(x)=sin^(-1)(1-x^2)+x * (1)/(√(1-(1-x^2)^2))* (-2x)`

`f'(x)=sin^(-1)(1-x^2)-(2x^2)/(√(1-(1-2x^2+x^4)))`

`f'(x)=sin^(-1)(1-x^2)-(2x^2)/(√(1-1+2x^2-x^4))`

`f'(x)=sin^(-1)(1-x^2)-(2x^2)/(√(2x^2-x^4))`