Question

Write the equation of the line that passes through the points (3, 6) and (5, 18) using function notation.

a
f(x) = 2x + 12

b
f(x) = 6x − 12

c
y = 2x + 12

d
y = 6x − 12

Answer 1

The answer would be B: F(x) = 6x - 12

This line passes through both given points.

Answer 2

First, we must find the slope using the equation

`\frac{y_(2)-y_(1) } {x_(2)-x_(1)}`

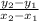
We can substitute in our points and will get

`(18-6)/(5-3) =(12)/(2) = 6`

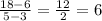
This means that our slope is m=6.

We can now use the point slope form to find the equation of the line. The equation for this is
`y-y_(1) =m(x-x_(1))`

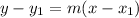
Now we can substitute in one of our point, (3,6) in this case.

`y-6 = 6(x-3)`

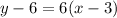
this simplifies to

`y= 6x-12`

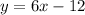
now we can swap y for f(x) to put it in function notation

this means that the answer is
`f(x) = 6x-12`; which means that the answer is b