Question

What equation results from completing the square and then factoring x^2+16x =41

A. (x+8)^2 =57

B.(x+16)^2 =57

C. (x+8)^2 =105

D. (x+16)^2 =105

Answer 1

C

given x² + 16x = 41

to complete the square on this equation

since the coefficient of the x² term is 1

add (half the coefficient of the x-term )² to both sides

x² + 2(8)x + 64 = 41+ 64

(x + 8 )² = 105 → C

Answer 2

Option C is correct

Explanation:

Given the equation

`x^2+16x=41`

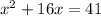
we have to find the equation results from completing the square.

For completing the square method, since the coefficient of
`x^2` is 1 therefore we have to divide the coefficient of x by 2 and then squaring of that value adding on both sides of equation, we get

Here coefficient of x is 16 therefore square of half the number adding both sides

`x^2+16x+64=41+64`

`x^2+8x+8x+64=105`

`x(x+8)+8(x+8)=105`

`(x+8)(x+8)=105`

`(x+8)^2=105`

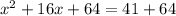
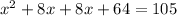
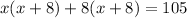
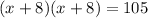
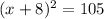
Option C is correct