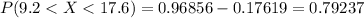Question

a distribution is normal with mu= 12.0 and sigma= 3.0. if i select one individual at random what is the probability that said individual is between 9.2 and 17.6

Answer 1

the probability between 9.2 and 17.6 is, 0.79237.

Step-by-step explanation:

It is given that distribution is normal.Also given the value of
`\mu = 12`

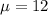
and
`\sigma = 3` .

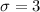Use :
`z = (x-\mu)/(\sigma)`

Now,

Calculate First
`P(X>9.2)`

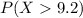
then we put the value of x =9.2 in the z transform,i.e,
`z = (x-\mu)/(\sigma)`

`z = (9.2-12)/(3)= -0.933333333`

Using the standard Normal table of N(0,1); we get

⇒
`P(X>9.2) = 0.17619`

Similarly, for
`P(X<17.6)`

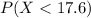
put the value of x =17.6 in the z-transform we get;

`z = (17.6-12)/(3)=1.86666667`

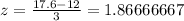
By the Normal Table N(0,1); we get

⇒
`P(X<17.6) = 0.96856`

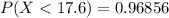
Then, the probability between 9.2 and 17.6 i.e,

`P(9.2<X<17.6) = 0.96856 - 0.17619=0.79237`