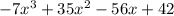Question

Third-degree, with zeros of 1-i, 1+i, and 3, and and a leading coefficient of -7

Answer 1

zeros of 1-i, 1+i, and 3

We need to find a third degree polynomial

if we are given with three zeros p, q and r then polynomial can be written as

a (x-p) (x-q) (x-r)

Leading coefficient is -7

So a= -7

Replace all the zeros

-7 ( x- 3) (x-(1-i)) (x-(1+i))

-7(x-3)(x-1+i) (x-1-i)

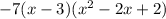`-7 (x - 3) (x^2 - 2 x + 2)` ( the value of i^2 = -1)

Multiply (x-3) inside the second parenthesis

`-7 (x^3 - 5 x^2 + 8 x - 6)`

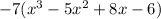
Now multiply -7 inside the parenthesis. the required polynomial is

`-7x^3 + 35x^2 - 56x + 42`