For this case we have the following data:
Slope,
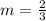
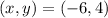
By definition, the equation of the slope-intercept form is given by:
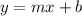
We must find the cut point b, for this we substitute the given point and the slope in the equation:
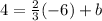
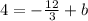
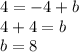
Thus, the equation is given by:

Now, we look for the points of intersection with the x and y axes respectively:
Point of intersection with the y axis:
We do
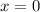 and substitute in the equation found:
and substitute in the equation found:
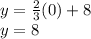
Thus, the point of intersection with the y-axis is (0,8).
Point of intersection with the x axis:
We make
 and substitute in the equation found:
and substitute in the equation found:
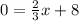
Clear x:
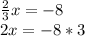
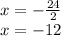
Thus, the point of intersection with the x-axis is (-12.0).
Answer:

See attached image