Answer:
Explanation:
Part A:
The length is given as =
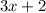 cm
cm
The width is give as = 10 cm
Area of rectangle = length x width
Area =
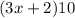
Given is that the area of the rectangle shown is at most of 140 square cm.
So, we can write this as:
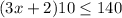
Solving this we get;
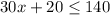
=>
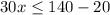
=>
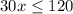
We get
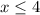
So,
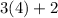 = 14 cm
= 14 cm
Hence, the length can be 14 cm and width is 10 cm.
Part B:
No, it is not possible as if the length will be 15, it will give an area of 150 cm square that is greater than 140 cm square.