vector A has magnitude 12 m and direction +y
so we can say
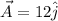
vector B has magnitude 33 m and direction - x

Now the resultant of vector A and B is given as
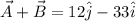
now for direction of the two vectors resultant will be given as
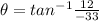
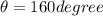
so it is inclined at 160 degree counterclockwise from + x axis
magnitude of A and B will be
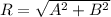
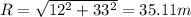
so magnitude will be 35.11 m