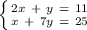
We can solve this system of equations by using the elimination method. This method works best for solving a system of equations if they are in the standard form, Ax + By = C, which these two equations are in.
Start by making the equations able to cancel out at least one of the terms (Ax or By). We will keep the first equation the same and change the second equation.
Multiply everything in the second equation by -2, so 2x and -2x cancel each other out. What I mean by "cancel" is that since they are opposites of each other (+ and -) they will add up to 0 and you are left with a one-step equation.
-2(x + 7y = 25) = -2x - 14y = -50
Now place the equations in order and add them.
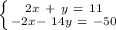
When adding opposites, 2x and -2x they cancel out, so now you are left with -13y = -39 after adding.
Divide both sides of the equation by -13 to isolate and solve for the variable y.
y = 3
You are left with the answer of y = 3. Substitute 3 for y into either one of the equations. I recommend the one with the least numbers, so I would substitute y into the first equation.
2x + (3) = 11
Subtract 3 from both sides.
2x = 8
Divide both sides by 2.
x = 4
Your answer to this system of equations is x = 4 and y = 3, so the answer is (4, 3).