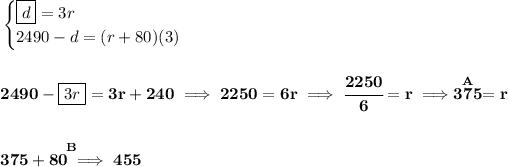Question

Two airplanes leave dallas at the same time and fly in opposite directions. One airplane travels 80 miles per hour faster then the other. After 3 hours,they are 2490 miles apart. What is the speed of each airplane?

Answer 1

recall d = rt, distance = rate * time.

let's say airplane A is going at a rate of "r", therefore airplane B is moving faster, at a rate of "r + 80".

now, after 3 hours, both planes have been travelling for 3 hours each, and say if A has covered "d" miles, then B has covered the slack of 2490 - d.

`\bf \leftarrow \underset{A}{\stackrel{r}{\rule[0.22em]{8em}{0.25pt}}}dallas\underset{B}{\stackrel{r+80}{\rule[0.22em]{18em}{0.25pt}}}\to \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{lcccl} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ \cline{2-4}&\\ plane~A&d&r&3\\ plane~B&2490-d&r+80&3 \end{array}`

`\bf \begin{cases} \boxed{d}=3r\\ 2490-d=(r+80)(3) \end{cases} \\\\\\ 2490-\boxed{3r}=3r+240\implies 2250=6r\implies \cfrac{2250}{6}=r\implies \stackrel{A}{375}=r \\\\\\ \stackrel{B}{375+80\implies 455}`