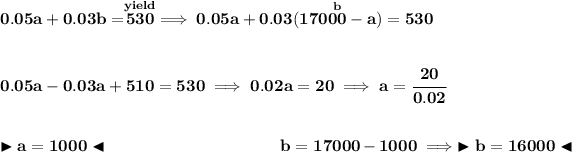bearing in mind that
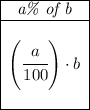
a = amount invested at 5%
b = amount invested at 3%
how much is 5% of "a"? well is simply (5/100) * a, or 0.05a.
how much is 3% of "b"? well is simply (3/100) * b or 0.03b.
we also know that "b" is the rest invested after "a" was invested, so since the total amount is 17000, then a + b = 17000, b = 17000 - a.
and since the yield or amount of both of those interests after the same year is 530, then