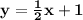Question

Write an equation of the line that passes through the given point and is (a) parallel and (b) perpendicular to the given line.

Answer 1

Equation of the line that passes through the given point and is (a) parallel is:
`\mathbf{y=-2x+11}`

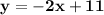
Equation of the line that passes through the given point and is (b) perpendicular is:
`\mathbf{y=(1)/(2)x+1}`

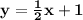
Explanation:

We need to Write an equation of the line that passes through the given point and is (a) parallel and (b) perpendicular to the given line.

First we will find slope of the line given in graph

The slope can be found using formula:
`Slope=(y_2-y_1)/(x_2-x_1)`

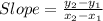
We have points (1,6) and (2,2)

Slope is:

`Slope=(y_2-y_1)/(x_2-x_1)\\Slope=(2-6)/(2-1)\\Slope=(-4)/(2)\\Slope=-2`

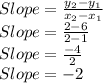
Part a)

Write an equation of the line that passes through the given point and is (a) parallel

When the lines are parallel, they have same slope. So, slope of required line: m = -2

Using slope m =-2 and point(4,3) we can find y-intercept b

`y=mx+b\\3=-2(4)+b\\3=-8+b\\b=3+8\\b=11`

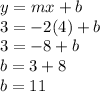
The equation of line will be:

`y=mx+b\\y=-2x+11`

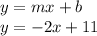
Equation of the line that passes through the given point and is (a) parallel is:
`\mathbf{y=-2x+11}`

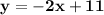
Part b)

Write an equation of the line that passes through the given point and is (b) perpendicular

When the lines are perpendicular they have opposite slope. So, slope of required line: m = 1/2

Using slope m =1/2 and point(4,3) we can find y-intercept b

`y=mx+b\\3=(1)/(2)(4)+b\\3=2+b\\b=3-2\\b=1`

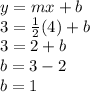
The equation of line will be:

`y=mx+b\\y=(1)/(2)x+1`

Equation of the line that passes through the given point and is (b) perpendicular is:
`\mathbf{y=(1)/(2)x+1}`