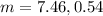Question

What is the sum of all values of m that satisfy 2m (squared) -16m+8=0?

Answer 1

Steps:

So for this, we will be completing the square to solve for m. Firstly, subtract 8 on both sides:

`2m^2-16m=-8`

Next, divide both sides by 2:

`m^2-8m=-4`

Next, we want to make the left side of the equation a perfect square. To find the constant of this perfect square, divide the m coefficient by 2, then square the quotient. In this case:

-8 ÷ 2 = -4, (-4)² = 16

Add 16 to both sides of the equation:

`m^2-8m+16=12`

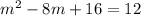
Next, factor the left side:

`(m-4)^2=12`

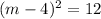
Next, square root both sides of the equation:

`m-4=\pm √(12)`

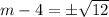
Next, add 4 to both sides of the equation:

`m=4\pm √(12)`

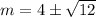
Now, while this is your answer, you can further simplify the radical using the product rule of radicals:

• Product rule of radicals: √ab = √a × √b

√12 = √4 × √3 = 2√3.

`m=4\pm 2√(3)`

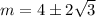
Answer:

In exact form, your answer is
`m=4\pm √(12)\ \textsf{OR}\ m=4\pm 2√(3)`

In approximate form, your answers are (rounded to the hundreths)
`m=7.46, 0.54`