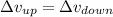Question

Now consider a new situation: The ball is thrown upward from the ground with an initial velocity that takes exactly the same time tBA = tAB = 0.45 s to pass by the window, with the ball moving up rather than down. Consider the ball’s slowdown during this time: Let v ′ B be the ball’s speed (do not confuse the speed with the velocity) as it passes the window’s bottom on the way up and let v ′ A be its speed as it passes the window’s top, also in its way up. How does the ball’s slowdown ∆vup = v ′ B − v ′ A compare to its speedup ∆vdown on the way down? 1. ∆vup < ∆vdown if the mass of the ball is less than 0.1 kg and ∆vup > ∆vdown if the mass of the ball is greater than 0.1 kg 2. ∆vup < ∆vdown. 3. ∆vup = ∆vdown. 4. ∆vup > ∆vdown if the mass of the ball is less than 0.1 kg and ∆vup < ∆vdown if the mass of the ball is greater than 0.1 kg

Answer 1

Here since we know that

`t_(BA) = t_(AB)`

this equation shows that there is no air resistance

so in that case the time taken by the object during it's accent must be equal to the time taken by object during decent

so if we are given that during the upward motion object passes the two points A and B then its change in speed is given as

`\Delta v_(up) = v'_B - v'_A`

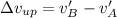
similarly if we take its downward motion then in that case

it will take same time to move through the two points

so we will have

`\Delta v = a \Delta t`

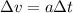
so here we will have

`\Delta v_(up) = \Delta v_(down)`