Question

Suppose a random sample of 347 married couples found that 197 had two or more personality preferences in common. In another random sample of 535 married couples, it was found that only 39 had no preferences in common. Let P subscript 1 be the population proportion of all married couples who have two or more personality preferences in common. Let P subscript 2 be the population proportion of all married couples who have no personality preferences in common. Find a 80% confidence interval for P subscript 1 minus end subscript P subscript 2

Answer 1

(0.4578 , 0.5318)

Explanation:

The attached figure shows the formula for calculating confidence intervals for the difference of proportions in large samples.

Let's call

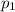`p_1` = proportion of married couples, in the first sample, who had two or more personality preferences in common.

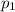`p_1` = 197/347 = 0.5677

`q_1 = 1-p_1`

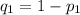
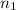`n_1` = size of the first random sample

`n_1 = 347`

`p_2` = proportion of married couples, in the second sample, who had no preferences in common.

`p_2` = 39/535 = 0.0729

`q_2 = 1-p_2`

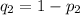
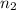`n_2` = size of the second random sample = 535

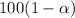`100 (1-\alpha)` = confidence%.

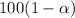`100 (1-\alpha)` = 80%

`(1-\alpha) = 0.8`

`\alpha = 0.2`

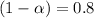
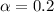
Looking in the normal standard table, we have that
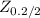`Z_ {0.2 / 2}` = 1.28.

Substituting this values ​​in the formula we have:

`0.5677-0.0729 + 1.28\sqrt{(0.5677(1-0.5677))/(347)+(0.0729(1-0.0729))/(535)}= 0.4948 + 0.03696\\\\ 0.5677-0.0729 - 1.28\sqrt{(0.5677(1-0.5677))/(347)+(0.0729(1-0.0729))/(535)}= 0.4948 - 0.03696`

`0.4948 + 0.03696 = 0.5318\\\\0.4948 - 0.03696 = 0.4578\\`

Then the confidence interval for p1-p2 is: (0.4578 , 0.5318)