Question

Use Remainder Theorem to determine if x-2 is a factor of the polynomial f(x)=3x^5 - 7x^3 -

11x^2 + 2

Answer 1

Answers to the Complex Zeroes of a Polynomial Function Quiz Part 1 (I tried to signify each question)

Explanation:

1. C, f(x) is a polynomial function. The degree is 5... -7

2. A, f(x)=7x^9-3x^2-6

3. C,D

4. Written

5. Rational Zero Theorem, B

6. Written

7. B, -5,-2, 3

8. A, (4 + 6i, -2 -11i)

9. D, (2,3, plus minus sqrt 5i)

Answer 2

(x - 2) is not a factor of f(x) = 3x^5 - 7x^3 - 11x^2 + 2

Explanation:

According to the Remainder Theorem, when a polynomial f(x) is divided by a term (x - r), then the remainder must be f(r).

So first we will divide f(x) by (x - 2) using long division to get:

(3x^5 - 7x^3 - 11x^2 + 2) / (x - 2)

= 3x^4 + (6x^4 - 7x^3 - 11x^2 + 2) / (x-2)

= 3x^4 + 6x^3 + (5x^3-11x^2+2) / (x - 2)

= 3x^4 + 6x^3 + 5x^2 (-x^2 + 2) / (x - 2)

= 3x^4 + 6x^3 + 5x^2 -x -2 - (2) / (x -2)

=
`(-2 + 3x^(5) - 7x^(3) - 11x^(2) + 2x)/(x - 2) - 2`

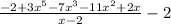
Therefore the remainder is -2.

Now check x = 2 for 3x^5 - 7x^3 - 11x^2 + 2:

3(2)^5 - 7(2)^3 - 11(2)^2 + 2 = -2

The Remainder Factor theorem also states that if (x - r) is a factor of f(x) then f(r) must be 0.

So we found that f(2) = -2, therfore (x - 2) is not a factor of f(x) .