To find the derivative of this function, there is a property that we should know called the Constant Multiple Rule, which says:
![(d)/(dx)[cf(x)] = cf'(x)](https://img.qammunity.org/2019/formulas/mathematics/middle-school/2nfb7l2doa5iu0as623x7m3ccfo4q7e508.png) (where
(where
 is a constant)
is a constant)
Remember that the derivative of
 is
is
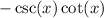 . However, you may notice that we are finding the derivative of
. However, you may notice that we are finding the derivative of
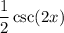 , not
, not
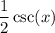 . So, we are going to have to use the chain rule. To complete the chain rule for the derivative of a trigonometric function (in layman's terms) is basically the following: First, complete the derivative of the trig function as you would if what was inside the trig function is
. So, we are going to have to use the chain rule. To complete the chain rule for the derivative of a trigonometric function (in layman's terms) is basically the following: First, complete the derivative of the trig function as you would if what was inside the trig function is
 . Then, take the derivative of what's inside of the trig function and multiply it by what you found in the first step.
. Then, take the derivative of what's inside of the trig function and multiply it by what you found in the first step.
Let's apply that to our problem. Right now, I am not going to worry about the
 at the front of the equation, since we can just multiply it back in at the end of our problem. So, let's examine
at the front of the equation, since we can just multiply it back in at the end of our problem. So, let's examine
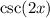 . We see that what's inside the trig function is
. We see that what's inside the trig function is
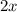 , which has a derivative of 2. Thus, let's first find the derivative of
, which has a derivative of 2. Thus, let's first find the derivative of
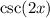 as if
as if
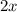 was just
was just
 and then multiply it by 2.
and then multiply it by 2.
The derivative of
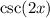 would first be
would first be
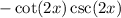 . Multiplying it by 2, we get our derivative of
. Multiplying it by 2, we get our derivative of
 . However, don't forget to multiply it by the
. However, don't forget to multiply it by the
 that we removed near the beginning. This gives us our final derivative of
that we removed near the beginning. This gives us our final derivative of
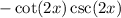 .
.
Remember that we now have to find the derivative at the given point. To do this, simply "plug in" the point into the derivative using the x-coordinate. This is shown below:
![-\cot[2((\pi)/(4))]\csc[2((\pi)/(4))]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/o7zii9vaa6ljkbu99p826uai7tvyj22mjz.png)
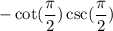
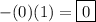
Our final answer is 0.