Object true weight is given as
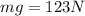
now we know that g = 9.8 m/s^2
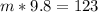
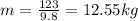
now when it is complete submerged in water its apparent weight is given as 82 N
apparent weight = weight - buoyancy force
apparent weight = 82 N
weight = 123 N
now we have
82 = 123 - buoyancy force
buoyancy force = 123 - 82 = 41 N
now we also know that buoyancy force is given as
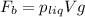

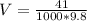
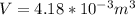
now as we know that mass of the object is 12.55 kg
its volume is 4.18 * 10^-3 m^3
now we know that density will be given as mass per unit volume
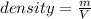
![density = \frac{12.55}{4.18*10^(-3)]()
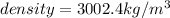
so here density of object is 3002.4 kg/m^3