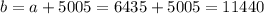Question

How to find a and b? (Pascal's triangle)

Answer 1

The two 5005s tell us we're in the middle of Pascal's triangle, which has bilateral symmetry.

So we can add the a and b labels to two other points by the symmetry as shown.

The two equations we can write are then

5005 + a = b

a + a = 12870

a = 12870/2 = 6435

b = 5005 + 6535 = 11540

Answer: a=6435, b=11540

Check:

Those are right, they happen to be

`{15 \choose 6} = {15 \choose 9} = 5005`

`{15 \choose 7} = {15 \choose 8} = 6435`

`{16 \choose 8}= 12870`

`{16 \choose 7} = {16 \choose 9} = 11440`

Answer 2

Pascal's triangle is symmetric, so the first line is actually

5005 a a 5005

and the second line is actually

. b 12870 b .

Moreover, in Pascal's triangle, each term is between two terms in the previous rows, and it turns out be their sum. So, you have

`2a = 12870 \iff a = 6435`

and also

`b = a+5005 = 6435+5005=11440`