Question

Plastic Box A has a square base of area 36 cm² and a height of 8 cm. It is completely filled with juice. Plastic Box B is empty and has dimensions 5 cm by 3 cm by 12 cm. Juice from Box A is poured into Box B until it is filled to the very top. Find the height of the new juice level in Box A.

Pls help me!!!❤️❤️❤️

Answer 1

3 cm

Explanation:

im not giving an explination just trust me its correct :)

Answer 2

Given: Box A (cube): square base of area 36 cm² and height of 8 cm

Box B (prism): 5 × 3 × 12

Box A is completely filled with juice and Box B is empty. Then, Box A is poured into Box B until filled.

First we find the volume (V) of both boxes: V = Bh (where B is the area of the base and h is the height)

Volume of Box A = 36 × 8 = 288
`cm^(3)`

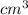
Base area of Box B = 5 × 3 = 15 cm²

Volume of Box B = 15 × 12 = 180
`cm^(3)`

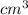
We know that the volume of Box A is greater than the volume of Box B

(V Box A = 288, V Box B = 180)

In order to find the new volume of juice in Box A after we pour it into Box B, we subtract the volume of Box B from the volume of Box A; since Box A is poured into Box B.

288 - 180 = 108
`cm^(3)`

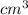
Now that Box B is filled completely, we find the height of the new juice level in Box A

108
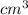`cm^(3)` is the amount of juice left in Box A

We know that the Base area of Box A is 36 cm²

In order to find the height of the new juice level in Box A, we use the new volume of the juice left in Box A (108
`cm^(3)`)

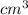∵ V = Bh

∴ h = V ÷ B

∴ 108 ÷ 36 = 3 cm

∴ The height of the new juice level in Box A = 3 cm