Question

Solve the system, please show each step.

x + y + z = -4
-x + 2y + 3z = 3
x - 4y - 2z = -15

Answer 1

The given equations are

x + y + z = -4

-x + 2 y + 3 z = 3

x - 4 y - 2 z = -15

Writing in matrix form

A= 1 1 1 X= x B= -4

-1 2 3 y 3 ⇒A,X,B are in matrix form.

1 -4 -2 z -15

i.e Ax=B

x =
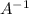`A^(-1)`B

but ,
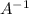`A^(-1)`=Adj.(A)/Determinant A

Determinant of A= 1(-4+12) -1(2-3)+1(4-2)=8+1+2=11

To find Adjoint of matrix A, we will find the cofactor of A and then it's transpose.

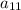`a_(11)`=-4+12=8,
`a_(12)=-[2-3]=1,`

`,a_(13)=4-2=2,\\,a_(21)=-[-2+4]=-2\\,a_(22)=-2-1=-3,\\a_(23)=-[-4-1]=5,\\a_(31)=[3-2]=1\\,a_(32)=-[3+1]=-4\\,a_(33)=2+1=3`

Now taking cofactor, and getting the adjoint

Adjoint (A)= 8 -2 1

1 - 3 -4

2 5 3

Adjoint(A). B= -53

47

-38

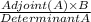`(Adjoint (A)* B)/(Determinant A)` = -53/11

47/11

-38/11

So, solution set is , x=-53/11, y=47/11, z=-38/11

Answer 2

Answer: The solution of the system of equations is
`x=(-53)/(11)`,
`y=(47)/(11)` and
`z=(-38)/(11)`.

Step-by-step explanation:

The given equations are,

`x+y+z=-4` ..... (1)

`-x+2y+3z=3` ..... (2)

`x-4y-2z=-15` ...... (3)

From equation we get,

`x=-4-y-z`

Put this value in equation (4) and (5).

`-(-4-y-z)+2y+3z=3`

`3y+4z=-1` .... (4)

`(-4-y-z)-4y-2z=-15`

`-5y-3z=-11` .....(5)

Use elimination method to solve the equations (4) and (5).

Multiply equation (4) by 3 and equation (5) by 4, then add both equations as shown in figure,

`-11y=-47`

`y=(47)/(11)`

Put this value in equation (4).

`3((47)/(11))+4z=-1`

`4z=-1-(141)/(11)`

`4z=(-11-141)/(11)`

`z=(-152)/(11* 4)`

`z=(-38)/(11)`

Put
`y=(47)/(11)` and
`z=(-38)/(11)` in equation (1).

`x+(47)/(11)+(-38)/(11)=-4`

`x+(9)/(11)=-4`

`x=(-44-9)/(11)`

`x=(-53)/(11)`

Therefore, the The solution of the system of equations is
`x=(-53)/(11)`,
`y=(47)/(11)` and
`z=(-38)/(11)`.