Question

Exponent Laws - difference between product law and product raised to a power (with formula please)

Answer 1

Exponent laws:

1. Product law

`x^(a)* x^(b)* x^(c)=x^(a+b+c)`

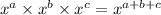
In product law if bases are same then we add their respective powers.But if bases are different we can't add their powers.

x=base, a,b,c=exponent

If x=2 and a=3, b=5 , and c=10, then

`2^(3)*2^(5)*2^(10)=2^(3+5+10)=2^(18)`

2.Product raised to a power

1.
`[x^(a)]^(c)=x^(ac)`

2.
`[x^(a)* x^(b)]^(c)=[x^(a+b)]^(c)=x^(ac+bc)`

If product is raised to a certain power , keeping the base same , we just multiply the powers.for example

`[2^(3)]^(4)=2^(3*4)=2^(12)` and

`[2^(3)*3^(2)]^(2)=[2^(3)]^2 *[3^(2)]^(2)=2^(6)*3^(4)`

`[2^(3)*2^(2)]^(2)=[2^(3+2)]^(2)=[2^(5)]^(2)=2^(10)`