Question

Factor the expression completely over the complex numbers. X3+5x2+9x+45

Answer 1

`x^3+5x^2+9x+45=x^2(x+5)+9(x+5)=(x+5)(x^2+9)=(*)\\\\x^2+9=x^2+3^2=x^2-(-1)(3^2)=x^2-(i^2)(3^2)=x^2-(3i)^2\\\\i=√(-1)\to i^2=-1\\\\(*)=(x+5)[x^2-(3i)^2]=(x+5)(x-3i)(x+3i)\\\\Used:\ a^2-b^2=(a-b)(a+b)\\\\Answer:\ x^3+5x^2+9x+45=(x+5)(x-3i)(x+3i)`

Answer 2

The expression after completely factorizing is given by:

`x^3+5x^2+9x+45=(x+5)(x+3i)(x-3i)`

Explanation:

We are given an algebraic expression in terms of the variable x as follows:

`x^3+5x^2+9x+45`

We are asked to factor the expression completely.

i.e. the expression is written as follows:

`x^3+5x^2+9x+45=x^2(x+5)+9(x+5)`

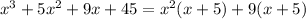
which is nothing but:

`x^3+5x^2+9x+45=(x^2+9)(x+5)`

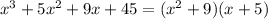
Now, we know that any quadratic equation of the type:

`ax^2+bx+c=0`

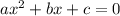
has solution by the quadratic formula as:

`x=(-b\pm √(b^2-4ac))/(2a)`

Here we have to find the solution of the quadratic equation:

`x^2+9=0`

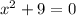
i.e.

`a=1,\ b=0\ and\ c=9`

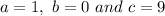
Hence, the solution is given by:

`x=(-0\pm √(0^2-4* 1* 9))/(2* 1)\\\\x=(\pm √(-36))/(2)\\\\x=(\pm 6i)/(2)\\\\x=\pm 3i\\\\x=3i\ and\ x=-3i\\\\x-3i=0\ and\ x+3i=0`

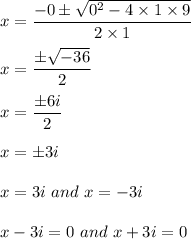
Hence, we have the expression as follows:

`x^3+5x^2+9x+45=(x+5)(x+3i)(x-3i)`