Question

I need help.
Math is really hard

Answer 1

The value of x in terms of b is:
`\mathbf{x=-(6)/(2b)}`

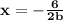
The value of x when b is 3 is: x = -1

Explanation:

We are given the function:
`-2(bx-5)=16`

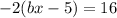
First we need to find

The value of x in terms of b

We need to find value of x

`-2(bx-5)=16`

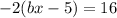
Multiply -2 with terms inside the bracket

`-2bx+10=16`

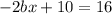
Subtract 10 from both sides

`-2bx+10-10=16-10\\-2bx=6`

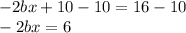
Divide both sides by -2b

`(-2bx)/(-2b)=(6)/(-2b)\\x=-(6)/(2b)`

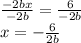
So, The value of x in terms of b is:
`\mathbf{x=-(6)/(2b)}`

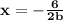
The value of x when b is 3

We have the equation for the value of x in terms of b:

`\mathbf{x=-(6)/(2b)}`

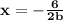
Put b = 3

`x=-(6)/(2(3))\\x=-(6)/(6)\\x=-1`

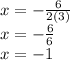
So, The value of x when b is 3 is: x = -1