Question

a normal population has a mean of u=21. after receiving a treatment a sample of n=4 scores yields the following data: 20,28,20,20. is there evidence for a significant treatment effect. use an alpha level of .05.

Answer 1

Calculate the z-score first.

`z = \frac{|\mu-\hat{\mu}|}{(s)/(√(n))}`

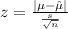
with "s" being the standard deviation within the sample of n=4 and
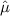`\hat\mu` being the sample mean.

So

`z=(|21-22|)/((4)/(2))=(1)/(2)`

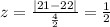
Note the absolute value - it takes care of a difference in both directions (sample mean being lower and higher) but we need to keep it mind when looking up the z values in tables - we must choose the "two-tailed test" table.

Now, look up the required z value for alpha=0.05: z>=1.96 (using a two-tailed table).

So our z would have be >=1.96 for the evidence to be significant at the required level of 0.05. The calculated value falls far short at 0.5. Therefore there is no evidence for a significant treatment effect, given the data/sample.