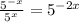Answer:
Josh claim is not correct.
Explanation:
Given : Josh examines the expression
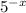 over
over
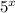 , where m is greater than 0.
, where m is greater than 0.
He claims that the expression has a value equal to 1 because it simplifies to
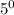 , and any integer to the 0 power is 1.
, and any integer to the 0 power is 1.
To find : Is Josh correct? Explain why or why not.
Solution :
We first solve the Josh expression,
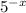 over
over
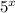
i.e.

We know,
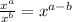
So,
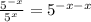
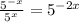
His claim is not correct.
As the correct solution is