Question

When given 2 data points, how would you use this information to create a linear equation? How would you create a linear equation if you were given an initial value and a rate of change? Use examples of your own to explain the process

Answer 1

Explanation:

A. When we are given two points we can find a linear equation by finding slope of the line and substituting it in point-slope form of equations.

Let (0,0) and (3,6) be two data points. Now we will find slope from these points.

`\text{Slope}=\frac{\text{Rise}}{\text{Run}}`

`\text{Slope}=(6-0)/(3-0) =(6)/(3) =2`

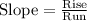
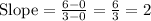
Now we will substitute our values in point-slope form of linear equations.
`(y-y_1)=m(x-x_1)`

`(y-6)=2(x-3)`

`y=2x-6+6`

`y=2x-6+6`

`y=2x`

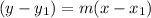
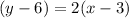
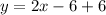
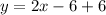
Therefore, our resulted linear equation will be
`y=2*x`

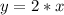
B. We will substitute the rate of change (slope) and initial value (y-intercept) into slope-intercept form of line to get the desired equation.

Let 4 be our initial value and -2 be our rate of change then,
`4=-2*x+b`

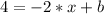
Substituting x=0 we will get value for b that is our y-intercept.

`4=-2*0+b`

`4=b`

`y=-2*x+4`

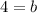
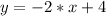
Therefore, our equation for line will be
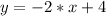`y=-2*x+4`.