1 Answer

Stephan Bauer · Answer 1 · 2019-10-08T17:36:14+0000

Answer-

The equations of the locus of a point that moves so that its distance from the line 12x-5y-1=0 is always 1 unit are

$12x-5y+14=0 \\ 12x-5y-14=0$

Solution-

Let a point which is 1 unit away from the line 12x-5y-1=0 is (h, k)

The applying the distance formula,

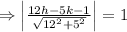
$\Rightarrow \left | (12h-5k-1)/(√(12^2+5^2)) \right |=1$

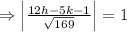
$\Rightarrow \left | (12h-5k-1)/(√(169)) \right |=1$

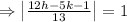
$\Rightarrow \left | (12h-5k-1)/(13) \right |=1$

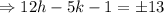
$\Rightarrow 12h-5k-1=\pm 13$

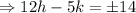
$\Rightarrow 12h-5k=\pm 14$

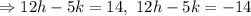
$\Rightarrow 12h-5k=14,\ 12h-5k=-14$

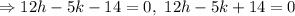
$\Rightarrow 12h-5k-14=0,\ 12h-5k+14=0$

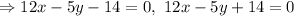
$\Rightarrow 12x-5y-14=0,\ 12x-5y+14=0$

Two equations are formed because one will be upper from the the given line and other will be below it.

Please log in or register to add a comment.