Question

98 pts to correct answer! CALCULUS BC Trig Substitution (SEE Attached)

Answer 1

The answer is 1.

Explanation:

The other solution is correct and good. I would like to show a different substitution and how it ends up with a different solution.

x/sqrt(x^2+1) = sqrt (x^2/(x^2+1))

=sqrt(1/(1+1/x^2))

=1/sqrt(1+1/x^2)

let x be cotΘ

dx=-csc^2ΘdΘ

1/x^2 = 1/cot^2Θ = tan^2Θ

x/sqrt(x^2+1)dx = 1/sqrt(1+1/x^2)dx

=1/sqrt(1+tan^2Θ) * (-csc^2Θ)dΘ

=-1/sqrt(sec^2Θ) * csc^2ΘdΘ

=-1/secΘ * csc^2ΘdΘ

=-cosΘ.csc^2ΘdΘ

I =
`\int\ -cos\theta\csc^2\theta\ \, d\theta\`

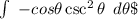
if plotted together, it is the same curve as for 1 but with Θ shifted by pi/2.

Answer 2

A

Explanation:

Let x = Tan
`(\theta)`

dx = sec²
`(\theta)`d
`(\theta)`

sqrt(1 +
`Tan^2(\theta)` ) = sec
`(\theta)`

So I = Tan(theta) * sec(theta)

but Tan(theta) = sin(theta) / cos(theta) = sin(theta)*sec(theta)

So I = integral sin(theta)*sec^2(theta) d theta

Answer A