Question

Suppose Alex is navigating using a compass. She starts walking at an angle of 60° north of east and walks a total of 100 m. How far north is she from the starting point? How far east?

Answer 1

`50\:\mathrm{m\: North}\\50√(3)\:\mathrm{m\: East}`

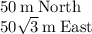
Step-by-step explanation:

We can create a 30-60-90 triangle. The distance she walked is then the hypotenuse of the triangle, and using 30-60-90 triangle rules, we have the following:

The North leg is opposite to the
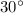`30^(\circ)` angle. Therefore, if we call this distance
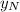`y_N`, we have the following:

`\sin 30^(\circ)=(y_N)/(100),\\(1)/(2)=(y_N)/(100),\\y_N=\fbox{$50\:\mathrm{m}$}`.

The East leg is opposite to the
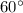`60^(\circ)\\` angle. If we call this distance
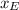`x_E`, we have:

`\sin 60^(\circ)=(x_E)/(100),\\(√(3))/(2)=(x_E)/(100),\\x_E=\fbox{$50√(3)\:\mathrm{m}$}`.