Solution-
The probability of making a single shot is,
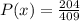
The probability of making 3 shot will be,
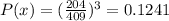
The probability of not making 3 shot is,
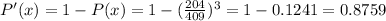
The expected gain for the basketball player will be,
= (Probability of making 3 shots) × ($17) + (Probability of NOT making 3 shots) x (-$4)
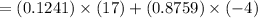
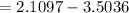
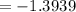

So the basketball player is expected to lose, on average, $1.39
If he played this game 921 times how much would you expect to win or lose
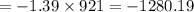
So the basketball player is expected to lose $1280.19, if he plays this game 921 times.