Answer: 5 (The second option).
Explanation:
1. To divide
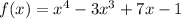 by
by
 you must complete the polynomial with the missing term
you must complete the polynomial with the missing term
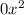 :
:
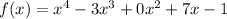
2. Write the coefficients of the polynomial and solve for
 in the deminator to find the number to write in the division:
in the deminator to find the number to write in the division:
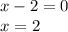
3. Write the first coefficient under the line, multiply 2 by this coefficient and substract the result with the next coefficient. Multiply the result of the substraction by 2 and repeat the proccedure this with each coefficient:
2 | 1 -3 0 7 -1
1 2 -2 -4 6
___________
-1 -2 3 5
4. The remainder is 5.