Question

Which systems of equations intersect at point A in this graph?

Answer 1

Answer: its the 2nd 4th and 5th one

Explanation:

i got it right on plato

Answer 2

The point of intersection of the system of equations is:

(x, y) = (-2, 1)

The correct system of equations intersect at point A in this graph will be:

`\begin{bmatrix}y=4x+9\\ y=-3x-5\end{bmatrix}`

Thus, the second option is correct.

Explanation:

Given the point

• A (-2, 1)

Let us check the system of equations to determine whether it intersect at point A in this graph.

Given the system of equations

`\begin{bmatrix}y=4x+9\\ y=-3x-5\end{bmatrix}`

Arrange equation variable for elimination

`\begin{bmatrix}y-4x=9\\ y+3x=-5\end{bmatrix}`

so

`y+3x=-5`

`-`

`\underline{y-4x=9}`

`7x=-14`

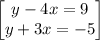
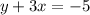
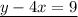
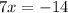
so the system of equations becomes

`\begin{bmatrix}y-4x=9\\ 7x=-14\end{bmatrix}`

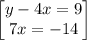
Solve 7x = -14 for x

`7x=-14`

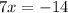
Divide both sides by 7

`(7x)/(7)=(-14)/(7)`

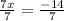
Simplify

`x = -2`

For y - 4x = 9 plug in x = 2

`y-4\left(-2\right)=9`

`y+4\cdot \:2=9`

`y+8=9`

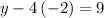
Subtract 8 from both sides

`y+8-8=9-8`

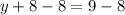
Simplify

y = 1

Thus, the solution to the system of equations is:

(x, y) = (-2, 1)

From the attached graph, it is also clear that the system of equations intersects at point x = -2, and y = 1.

In other words, the point of intersection of the system of equations is:

(x, y) = (-2, 1)

Therefore, the correct system of equations intersect at point A in this graph will be:

`\begin{bmatrix}y=4x+9\\ y=-3x-5\end{bmatrix}`

Thus, the second option is correct.