Alright, lets get started.

Distributing
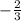 into parenthesis
into parenthesis
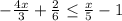
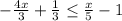
Subtracting
 from both sides
from both sides


Adding
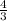 in both sides
in both sides

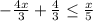
Adding
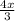 in both sides
in both sides
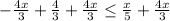
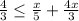
Making common denominator, adding fractions
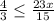
It means

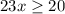
Dividing 23 in both sides
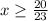
In interval notation
[
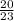 ,∞)
,∞)
This is the answer
Hope it will help :)