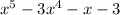Answer:
(x - 4) is not a factor because
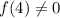 .
.
Explanation:
According to the factor theorem, if f(x) = 0, only then f(x) can have a factor (x-a) which in this case is equal to (x - 4).
Considering this factor theorem, we can write it as:

Now to check if (x - 4) is its factor or not, substitute a value of 4 in place of x in f(x):
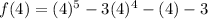

So f(x) is not equal to zero which means (x - 4) is not a factor of