Question

How do I get started on 15?

Answer 1

from the slope-intercept form of y = 3x - 4, we can see that the slope is 3 for that line, now if that line is going to be tangential to the curve x² + kx, then the slope of x² + kx must also be 3 at that point.

so let's get the derivative of f(x), bearing in mind that it has to be 3 in order to have a tangent line with a slope of 3 at that point.

`\bf \stackrel{f(x)}{y}=x^2+kx\implies \cfrac{dy}{dx}=2x+k\implies \stackrel{\textit{with a slope of 3}}{3=2x+k}\implies \boxed{3-2x=k}\\\\[-0.35em]~\dotfill\\\\\stackrel{\textit{if we plug that found \underline{k} into f(x)}}{y=x^2+(3-2x)x}\implies y=x^2+3x-2x^2\implies \boxed{y=3x-x^2}\\\\[-0.35em]~\dotfill\\\\\stackrel{\textit{and since both equations must equal each other at that point}}{\stackrel{tangent}{3x-4}=\stackrel{f(x)}{3x-x^2}\implies -4=-x^2\implies 4=x^2}\implies \boxed{\pm 2 = x}`

now, we already know that 3 - 2x = k, so let's simply plug that found "x" to see what "k" may be then.

`\bf 3-2x=k\implies 3-2(\pm 2)=k\implies 3\pm 4=k\implies k=\begin{cases}7\\-1\end{cases}\\\\\\therefore~\hspace{5em}f(x)=\begin{cases}x^2+7x\\x^2-x\end{cases}`

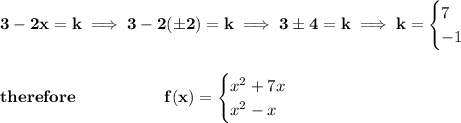
check the picture below.

Answer 2

y = 3x-4 _(1) ; f (x) =x^2 + kx _(2)

Find,

1. Slope of line i.e, 3

2. Slope of tangent to Curve f(x) i.e, f'(x) = 2x + k

Line (1) is tangent to curve (2)

》3 = 2x + k