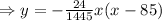Question

when hope kicked the soccer ball, it traveled a horizontal distance of 85 feet, and its highest reached 30 feet. write an equation to model the path of the soccer ball.

Answer 1

The equation for the trajectory of the ball is,

`y=-(24)/(1445)x(x-85)`

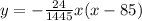
Solution-

The trajectory of the soccer ball, when kicked, will be a parabola.

Let's assume that the point where the ball was kicked as origin (0, 0)

Then the position of the ball where it landed would be (85, 0)

And the maximum height, which is 30, it reached would be halfway between these two points. So, the coordinates of highest point would be

`=((0+85)/(2),\ 30) =((85)/(2),\ 30)`

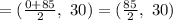
So,

`y((85)/(2))=30`

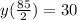
As a second degree polynomial function with zeros at x=0 and x=85/2, the function can be written in factored form as,

`\Rightarrow y=k(x-0)(x-85)`

`\Rightarrow y=kx(x-85)`

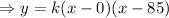
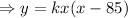
where k is constant and its value can be determined by putting the values of x and y. As we know the coordinates of highest point and that will satisfy the curve equation, so

`\Rightarrow 30=k((85)/(2))((85)/(2)-85)`

`\Rightarrow 30=k((85)/(2))(-(85)/(2))`

`\Rightarrow 30=k(-(7225)/(4))`

`\Rightarrow k=-(30* 4)/(7225)`

`\Rightarrow k=-(24)/(1445)`

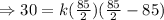
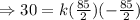
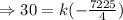
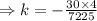
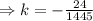
Then putting the value of k in the main equation,

`\Rightarrow y=-(24)/(1445)x(x-85)`