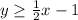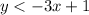Question

What system of linear inequalities is shown in the graph?
Enter your answers in the boxes.

Answer 1

The line equation in slope-intercept form is y=mx+b

You have one line with a y-intercept at 1 and a slope of -3 -> y=-3x+1

and another with a y-intercept at -1 and a slope of
`(1)/(2)` ->
`y=(1)/(2)x-1`

The area marked is below the first line and above the second one -> replace = with < and >:

y<-3x+1

`y>(1)/(2)x-1`

Which is the system of linear inequalities shown in the graph

Answer 2

`y\geq (1)/(2)x-1`

`y<-3x+1`

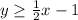
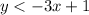
Explanation:

To find the system of linear inequalities, we first have to find the equation for each line. Which we do by finding first the slope, and then using the point-slope formula.

Line 1.

Using (0,-1) and (2,0) to find the slope:

`m=(0-(-1))/(2-0)=(1)/(2)`

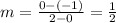
Then, using the point-slope formula:

`y-y_(1)=m(x-x_(1))\\  y-0=(1)/(2)(x-2)\\y=(1)/(2)x-1`

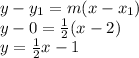
Line 2.

Using (0,1) and (1,-2), we have:

`m=(-2-1)/(1-0)=-3`

`y-y_(1)=m(x-x_(1))\\y-(-2)=-3(x-1)\\y=-3x+3+-2\\y=-3x+1`

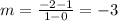
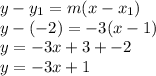
Now we have each equations, we just have to find which area is solution ofr each one.

We see that the area of solutions is above line 1, and below line 2. To demonstrate this better, we take the point (0,0), as testing point.

`y\geq (1)/(2)x-1\\0\geq (1)/(2)0-1\\0\geq -1`

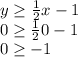
This result is true, so the first inequality is:
`y\geq (1)/(2)x-1`

`y<-3x+1\\0<-3(0)+1\\0<1`

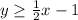
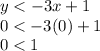
Which is also true, so the second inequality is:
`y<-3x+1`

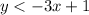
Observe that the inequality sign that refers to "less or equal than" represent a solid line, and "less than" a not solid line.

Therefore, the system is formed by:

`y\geq (1)/(2)x-1`

`y<-3x+1`