Answer:
Then point P is (
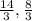 )
)
The correct answer is option 2.
Explanation:
First let's calculate the distance between points A and B
A: (4.0)
B: (6.8)
The distance in x between both is:

The distance in the y axis between both is:
 .
.
We know that the point divides the line segment in a 1: 2 ratio as shown in the following diagram
A --------- P ------------------- B
Where the distance PB is twice as large as the AP distance.
Then

Therefore Point P is at a distance d = 1/3 * (
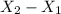 ) from point A.
) from point A.
So:
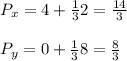
Then point P is (
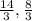 )
)
The correct answer is option 2.