Answer (this one's written in slope-intercept form):

Explanation:
1) Lines that are parallel to each other have the same slope. The line
 is in slope intercept form, or
is in slope intercept form, or
 form, and the number in place of
form, and the number in place of
 represents the slope. Knowing this, it looks like
represents the slope. Knowing this, it looks like
 is in the place of the
is in the place of the
 in that equation, so
in that equation, so
 is the slope - and the slope we need to use for the answer, too.
is the slope - and the slope we need to use for the answer, too.
2) Once you know a point that the line must pass through and a slope, you can write an equation with point-slope form, or
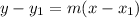 .
.
 is the slope and
is the slope and
 and
and
 are the x and y values of the point it must pass through. So, substitute
are the x and y values of the point it must pass through. So, substitute
 for
for
 , 0 for
, 0 for
 , and -3 for
, and -3 for
 . Simplify and isolate y to put it in slope-intercept form:
. Simplify and isolate y to put it in slope-intercept form:
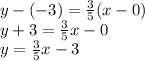
3) Thus,
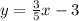 is the answer. It's written in slope-intercept form.
is the answer. It's written in slope-intercept form.