Question

△MNO is rotated about point A to △M′N′O′ . Which statements are true about the pre-image and image? Select each correct answer. The image is the same shape but a different size than the pre-image. MN¯¯¯¯¯¯¯≅M′N′¯¯¯¯¯¯¯¯¯ ∠NOM≅∠N′O′M′ The image is the same size but a different shape than the pre-image.

Answer 1

Only the two hold:

MN≅M′N′

∠NOM≅∠N′O′M′

Both the size and shape are the same so the other choices are out.

Answer 2

Answer:
`\overline{MN}\cong\overline{M'N'}`

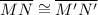
∠NOM≅∠N′O′M′

Explanation:

A rotation is a rigid transformation that produces congruent images ,

i.e. The image has the same size and shape as the pre-image.

i.e. it preserves the side length and of the pre-image.

If △MNO is rotated about point A to △M′N′O′ , then △MNO≅△M′N′O′

Since ,
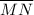`\overline{MN}` and
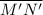`\overline{M'N'}` are corresponding sides and ∠NOM are ∠N′O′M′ corresponding angles

⇒
`\overline{MN}\cong\overline{M'N'}`

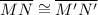
and ∠NOM≅∠N′O′M′

Hence, the statements are true about the pre-image and image :

`\overline{MN}\cong\overline{M'N'}`

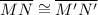
∠NOM≅∠N′O′M′