Answer:
The probability that 10 or more students will live in campus housing is approximately 0.111%
Explanation:
Binomial distribution formula:
If the probability of success is
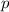 , then the probability of
, then the probability of
 successes out of
successes out of
 trials will be:
trials will be:
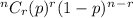
26% of college students live in campus housing. So here,
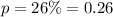
A random sample of 15 college students is selected. So,

Now, "10 or more students" means 10 or 11 or 12 or 13 or 14 or 15 students. That means,
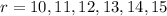
Thus, the probability that 10 or more students will live in campus housing will be........
![[^1^5C_(10)(0.26)^1^0(1-0.26)^5]+[^1^5C_(11)(0.26)^1^1(1-0.26)^4]+[^1^5C_(12)(0.26)^1^2(1-0.26)^3]+[^1^5C_(13)(0.26)^1^3(1-0.26)^2]+[^1^5C_(14)(0.26)^1^4(1-0.26)^1]+[^1^5C_(15)(0.26)^1^5(1-0.26)^0]\\ \\ = 0.00094...+0.00015...+0.00001...+ 0.0000014...+ 0.000000071...+0.0000000016...\\ \\ =0.00111002... =0.111002...\% \approx 0.111\%](https://img.qammunity.org/2019/formulas/mathematics/middle-school/oy9qpim8rp4d5y7z7px8m5i0vfq32zxgar.png)