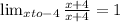Explanation:
What you get when you take the graph over to a place like Desmos is a straight line. The question is what happens at x + 4 or x = - 4? Let's do the rest of it first. Factor f(x) = [x^2 + 9x + 20] / (x + 4)
f(x) = [(x + 5)(x + 4)] / (x + 4)
The graph looks like f(x) = (x + 5)
That's fine for every point on the graph except x = - 4. That gives you 0/0 which is always a problem. The point seems to be continuous but I think it should be noted as something special.
If you know what limits are, then you can write it like this
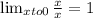
Similarly