Question

What are the coordinates of the orthocenter of △JKL with vertices at J(−4, −1) , K(−4, 8) , and L(2, 8) ?

Answer 1

The coordinates of the orthocenter of △JKL is (-4, 8)

Solution-

The orthocenter is the point where all three altitudes of the triangle intersect. An altitude is a line which passes through a vertex of the triangle and is perpendicular to the opposite side.

For a right angle triangle, the vertex at the right angle is the orthocentre of the triangle.

Here we are given the three vertices of the triangle are J(-4,-1), K(-4,8) and L(2,8)

If the triangle JKL satisfies Pythagoras Theorem, then triangle JKL will be a right angle triangle.

Applying distance formula we get,

`JK^2= (-4+4)^2+ (8+1)^2=0+81=81\\\\KL^2= (-4-2)^2+ (8-8)^2=36+0=36\\\\JL^2= (-4-2)^2+(8+1)^2=36+81=117`

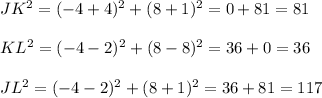
As,

`\Rightarrow 117=81+36`

`\Rightarrow JL^2=JK^2+KL^2`

`\Rightarrow \text{JKL is a right angle triangle}`

`\Rightarrow \angle K=90^(\circ)`

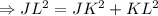
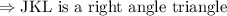
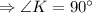
Therefore, the vertex at K (-4, 8) is the orthocentre.