Question

Find the standard form of the equation of the hyperbola x2 − 4y2 − 2x + 16y − 31 = 0. Place the signs and values in the correct places in the standard form of the equation.

- + 1 2 4 5

Answer 1

B

Explanation:

plato

Answer 2

Given equation:
`x^2 - 4y^2 - 2x + 16y - 31 = 0.`

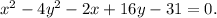
Making it into groups of x and y terms.

( x^2-2x ) + (-4y^2 +16y ) -31 =0

Adding 31 on both sides.

( x^2-2x ) + (-4y^2 +16y ) =31.

Factoring of -4 from second group.

( x^2-2x ) -4 (y^2 - 4y ) = 31.

Completing the squares

(x^2 -2x +1) - 4(y^2 -4y +4)

We added 1 in first parenthesis and -4*4 = -16 in second parenthesis.

Adding 1 and -16 on right side too, we get

(x^2 -2x +1) - 4(y^2 -4y +4) = 31+1 -16

Making perfect squares

(x-1)^2 - 4(y-2)^2 = 16.

Dividing both sides by 16, we get

`((x-1)^2)/(16)-(4(y-2)^2)/(16)=(16)/(16)`

`((x-1)^2)/(16)-((y-2)^2)/(4)=1`.

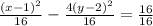
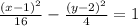Therefore, final equation of hyperbola in standard form is \frac{(x-1)^2}{16}-\frac{(y-2)^2}{4}=1