Question

You are the operations manager for an airline and you are considering a higher fare level for passengers in aisle seats. How many randomly selected air passengers must you​ survey? Assume that you want to be 90​% confident that the sample percentage is within 5.5 percentage points of the true population percentage. Assume that nothing is known about the percentage of passengers who prefer aisle seats.

Answer 1

Solution: We are given:

Margin of error
`E=0.055`

Confidence level
`=90\%`

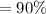
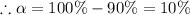`\therefore \alpha =100\%-90\%=10\%` or
`0.1`

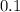
Since we are not given the proportion of passengers who prefer aisle seats, therefore we assume it to be
`0.5`

`\therefore p=0.5`

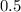
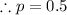
Now, the formula for finding the sample size is:

`n=p(1-p)\left( \frac{z_{\frac{0.1} {2}} }{E} \right)^(2)`

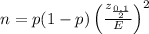
Where:

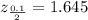`z_{(0.1)/(2)}=1.645` is the critical value at 0.1 significance level

`\therefore n=0.5(1-0.5) \left((1.645)/(0.055)\right)^(2)`

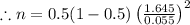
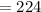`=224` rounded to nearest integer