Answer:
Let x be the speed of current ( miles per hour ),
Thus, as per statement,
The speed of boat in still water = 5x miles per hour,
⇒ The speed in upstream = 5x - x = 4x miles per hour,
And, the speed in downstream = 5x + x = 6x miles per hour,
We know that,

Given distance = 12 miles,
So, the time taken in upstream =

And, the time taken in downstream =
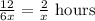
Total time taken = 2½ hours
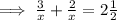
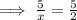

Hence, the speed of current is 2 miles per hour.