Answer:
The perimeter is 72 units and the area is 149 square units.
Explanation:
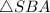 has coordinates
has coordinates
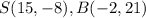 and
and
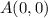
Using the distance formula.........
Length of side
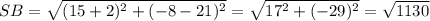
Length of side
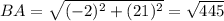
Length of side
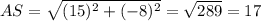
So, the perimeter of the triangle will be:
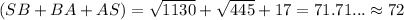 units. (Rounded to the nearest unit)
units. (Rounded to the nearest unit)
The height of the triangle for the corresponding base
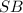 is 8.89 units.
is 8.89 units.
Formula for the Area of triangle,
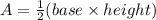
So, the area of the
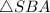 will be:
will be:
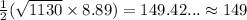 square units. (Rounded to the nearest unit)
square units. (Rounded to the nearest unit)